The goal is to determine how many of each cabin type to allocate to the different demand slots to maximize revenues.

Data

We begin by analysing our data:

Model Construction

To solve this problem optimally, we will formulate and solve an integer programming (IP) model to allocate capacity to the demand forecast in a way that maximizes the revenue attained. This model assigns cabins to demand slots in the form of (time interval, cabin size) pairs and employs binary indicators to enable specification of allowable substitutions. We begin by defining the model inputs:

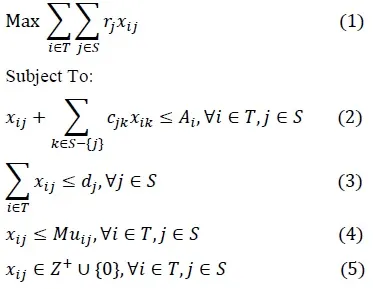
In the model above, the objective function (1) is simply the sum of all revenue attained over the period. Constraints in (2) ensure that we never overbook the available capacity for any cabin type. We do this by ensuring that for any cabin type i and slot j , the total number of type i cabins assigned either to slot j or any other slot that overlaps j’s start time does not exceed the number of type i cabins available. Constraints in (3) ensure we don’t allocate more cabins than demand for any slot. Constraints in (4) ensure that we never make invalid substitutions by assigning cabins to slots they cannot satisfy. Finally, constraints in (5) ensure non-negative integer domains for the decision variables.

Obtaining an Optimal Capacity Allocation Plan

Now we will create an optimize function to solve the model, which will determine our optimal sales plan and revenue attained. To accomplish this, we first need to create a few helper functions to transform our raw data into the format needed by the model.

As we look at this optimal allocation plan, we note the many instances of substituting larger cabins for smaller ones that occur. As we will see, allowing these kinds of substitutions can have a big impact on revenues.

Model Construction

For the modeling the Problem, we will formulate and solve an integer programming (IP) model to allocate capacity to the demand forecast in a way that maximizes the revenue attained. This model assigns cabins to demand slots in the form of (time interval, cabin size) pairs and employs binary indicators to enable specification of allowable substitutions. We begin by defining the model inputs:

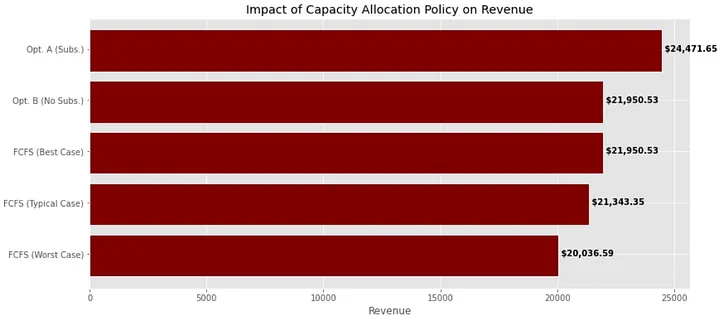
Comparing policies, we see that FCFS will typically leave revenue on the table — and if we get unlucky, this can be a significant amount. Only in the best case will FCFS reach the maximum revenue possible under the assumption of no substitutions allowed (which is always reached by the Optimization B policy). By allowing substitutions and optimizing, however, we attain a big boost in revenues — amounting to an increase of more than 22% over the worst-case (or well over $4,000) for the weekend. Moreover, this extra revenue is earned using existing capacity without incurring any additional costs, so it is entirely profit. This comparison demonstrates the impact RM can make.

As a final caveat, we point out that effective capacity allocation relies on good demand forecasts to use as optimization inputs. Some weeks our forecast will miss the mark. However, assuming forecasts can be typically made with reasonable accuracy, systems that use RM will in the aggregate outperform those that don’t.

Solution: First Come, First Served

To provide comparison, we will implement a first-come-first-served (FCFS) algorithm to mimic the way a human agent not using RM would most likely allocate the capacity. In FCFS, booking requests are served as they come in if there is available capacity to meet them. Substituting larger cabins for smaller is not used since, without a demand forecast, we would not know whether the next request might be for a larger, higher-paying cabin.

Conclusion

Revenue Management is a science that can significantly increase revenues attained with existing capacity. By incorporating the elements of RM into the sales process, companies can begin to increase revenues without incurring additional operational costs.

Have a Question ?

Whether you are a small business owner or a large enterprise, our data analytics solutions can help you stay ahead of the curve and make informed decisions that drive business growth and success. Contact us today to learn more about how our services can benefit your organization!